機械学習手習い: 主成分分析を使った株価指標の作成
「入門 機械学習」手習い、8日目。「8章 PCA:株式市場指標の作成」です。
PCA(principal components analysis)とは、日本語で主成分分析のことで、 多数のデータを「縮約」して、傾向を表す少数の指標を作成することを指します。 今回は、主成分分析を使って、複数銘柄の株価データから、全体の傾向を要約した株価指標を作成してみます。
前準備とデータの読み込み
株価データを読み込み。
> setwd("08-PCA") > library('ggplot2') > prices <- read.csv(file.path('data', 'stock_prices.csv'), stringsAsFactors = FALSE) > head(prices) Date Stock Close 1 2011-05-25 DTE 51.12 2 2011-05-24 DTE 51.51 3 2011-05-23 DTE 51.47 4 2011-05-20 DTE 51.90 5 2011-05-19 DTE 51.91 6 2011-05-18 DTE 51.68
日付が文字列になっているので、日付オブジェクトに変換します。
> library('lubridate') > prices <- transform(prices, Date = ymd(Date))
銘柄間の相関を確認する
主成分分析では、各データごとの相関が強いときに効果が大きくなります。
まずは、各データの相関を確認します。
> library('reshape') # 一部データに欠落があるので、除外 > prices <- subset(prices, Date != ymd('2002-02-01')) > prices <- subset(prices, Stock != 'DDR') # 日付を行、銘柄を列とするマトリックスに変換 > date.stock.matrix <- cast(prices, Date ~ Stock, value = 'Close') > head(date.stock.matrix) Date ADC AFL ARKR AZPN CLFD DTE ENDP FLWS FR GMXR GPC 1 2002-01-02 17.70 23.78 8.15 17.10 3.19 42.37 11.54 15.77 31.16 4.50 36.09 2 2002-01-03 16.14 23.52 8.15 17.41 3.27 42.14 11.48 17.40 31.45 4.37 35.90 3 2002-01-04 15.45 23.92 7.79 17.90 3.28 41.79 11.60 17.11 31.46 4.45 35.60 4 2002-01-07 16.59 23.12 7.79 17.49 3.50 41.48 11.90 17.38 31.10 4.38 35.83 5 2002-01-08 16.76 25.54 7.35 17.89 4.24 40.69 12.41 14.62 31.40 4.30 36.00 6 2002-01-09 16.78 26.30 7.40 18.25 4.25 40.81 12.27 14.27 31.05 4.25 36.20 HE ISSC ISSI KSS MTSC NWN ODFL PARL RELV SIGM STT TRIB UTR 1 40.41 7.82 12.78 70.23 10.03 26.20 13.40 1.92 1.30 1.75 52.11 1.50 39.34 2 40.53 7.29 13.40 69.65 10.85 26.25 13.00 1.94 1.22 2.11 52.90 1.55 39.49 3 40.54 6.90 14.16 70.21 10.34 26.46 13.00 1.98 1.26 2.20 54.16 1.54 39.38 4 40.25 6.30 13.81 70.17 9.99 26.84 13.32 1.94 1.28 2.11 55.14 1.55 38.55 5 39.88 6.83 14.05 69.90 10.35 27.35 13.75 1.94 1.27 2.25 54.44 1.58 38.98 6 39.90 7.00 14.15 69.01 10.15 26.15 13.74 1.97 1.28 2.16 54.92 1.64 39.60
Date列を除いた、他のすべての列の相関係数を総当たりで算出。
# Date列を除いた、他のすべての列の相関係数を総当たりで算出。 > cor.matrix <- cor(date.stock.matrix[, 2:ncol(date.stock.matrix)]) # マトリックスになっているので、数値のベクトルに変換 > correlations <- as.numeric(cor.matrix) # ヒストグラムを描く > ggplot(data.frame(Correlation = correlations), aes(x = Correlation, fill = 1)) + geom_density() + theme(legend.position = 'none') > ggsave(filename="histogram.png")
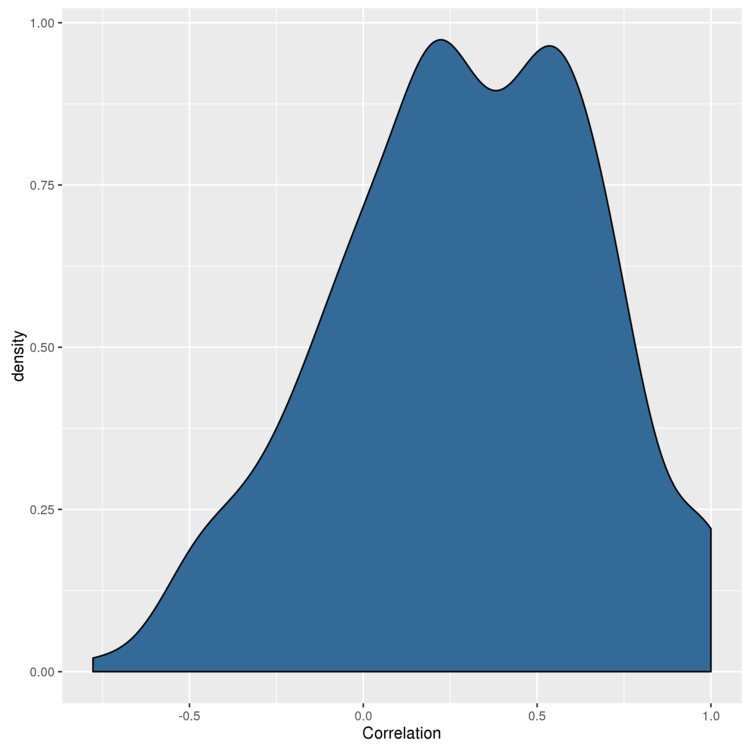
ピークは正の値になっているので、主成分分析はうまくいきそうです。
主成分分析を行う
Rでは princomp 関数で主成分分析が行えます。
> pca <- princomp(date.stock.matrix[, 2:ncol(date.stock.matrix)]) > pca Call: princomp(x = date.stock.matrix[, 2:ncol(date.stock.matrix)]) Standard deviations: Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 29.1001249 20.4403404 12.6726924 11.4636450 8.4963820 8.1969345 5.5438308 Comp.8 Comp.9 Comp.10 Comp.11 Comp.12 Comp.13 Comp.14 5.1300931 4.7786752 4.2575099 3.3050931 2.6197715 2.4986181 2.1746125 Comp.15 Comp.16 Comp.17 Comp.18 Comp.19 Comp.20 Comp.21 1.9469475 1.8706240 1.6984043 1.6344116 1.2327471 1.1280913 0.9877634 Comp.22 Comp.23 Comp.24 0.8583681 0.7390626 0.4347983 24 variables and 2366 observations. > summary(pca) Importance of components: Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Standard deviation 29.1001249 20.4403404 12.67269243 11.46364500 8.49638196 Proportion of Variance 0.4600083 0.2269615 0.08723961 0.07138737 0.03921426 Cumulative Proportion 0.4600083 0.6869698 0.77420941 0.84559678 0.88481104 Comp.6 Comp.7 Comp.8 Comp.9 Comp.10 Standard deviation 8.19693448 5.54383078 5.13009309 4.77867520 4.257509927 Proportion of Variance 0.03649882 0.01669536 0.01429639 0.01240483 0.009846622 Cumulative Proportion 0.92130986 0.93800523 0.95230162 0.96470645 0.974553074 Comp.11 Comp.12 Comp.13 Comp.14 Standard deviation 3.305093119 2.619771465 2.498618085 2.174612539 Proportion of Variance 0.005933943 0.003728231 0.003391374 0.002568856 Cumulative Proportion 0.980487017 0.984215247 0.987606622 0.990175477 Comp.15 Comp.16 Comp.17 Comp.18 Standard deviation 1.946947496 1.870623998 1.698404287 1.634411605 Proportion of Variance 0.002059133 0.001900855 0.001566961 0.001451105 Cumulative Proportion 0.992234610 0.994135465 0.995702426 0.997153531 Comp.19 Comp.20 Comp.21 Comp.22 Standard deviation 1.232747064 1.1280913254 0.9877633997 0.8583681320 Proportion of Variance 0.000825513 0.0006912967 0.0005300072 0.0004002424 Cumulative Proportion 0.997979044 0.9986703406 0.9992003478 0.9996005903 Comp.23 Comp.24 Standard deviation 0.7390625523 0.4347982692 Proportion of Variance 0.0002967142 0.0001026955 Cumulative Proportion 0.9998973045 1.0000000000
Comp.1 Comp.2 ... が主成分で、寄与率(Proportion of Variance) が、その主成分でデータ全体のどの程度を説明できているかを示します。累積寄与率(Cumulative Proportion) は、寄与率を蓄積した値で、↑の場合なら Comp.1,Comp.2を使うと、データの68.6%を説明できます。
第一主成分(Comp1)がどのようにできているかは、loadingsで負荷を取り出すことで調べることができます。
> principal.component <- pca$loadings[, 1] > principal.component ADC AFL ARKR AZPN CLFD DTE -0.160756643 -0.269577636 -0.313489533 -0.071623993 0.012445236 -0.085272822 ENDP FLWS FR GMXR GPC HE -0.185242688 -0.018440018 -0.270140267 -0.448622161 -0.169911152 0.132789793 ISSC ISSI KSS MTSC NWN ODFL -0.139360089 0.007478053 -0.041249777 -0.309455606 -0.126452792 -0.040702588 PARL RELV SIGM STT TRIB UTR -0.126541135 -0.080583114 -0.271218212 -0.366492421 -0.076298673 -0.253900525
元データの各列の値に↑の負荷を掛けて合計した値が、第一主成分です。
第一主成分で要約した値を算出する
今回は、第一主成分のみを使うことにします。
predictを使って、第一主成分でデータを要約したものを生成します。
> market.index <- predict(pca)[, 1] > head(market.index) [1] 30.11593 29.87794 29.68801 29.77801 28.97101 28.73909
ダウ平均株価と比較してみる
第一主成分で要約した値を、ダウ平均株価と比較してみます。
#ダウ平均株価を読み込み > dji.prices <- read.csv(file.path('data', 'DJI.csv'), stringsAsFactors = FALSE) > dji.prices <- transform(dji.prices, Date = ymd(Date)) # 分析対象外のデータが含まれているので除外 > dji.prices <- subset(dji.prices, Date > ymd('2001-12-31')) > dji.prices <- subset(dji.prices, Date != ymd('2002-02-01')) > head(dji.prices) Date Open High Low Close Volume Adj.Close 1 2011-05-25 12355.45 12462.28 12271.90 12394.66 4109670000 12394.66 2 2011-05-24 12381.87 12465.80 12315.42 12356.21 3846250000 12356.21 3 2011-05-23 12511.29 12511.29 12292.49 12381.26 3255580000 12381.26 4 2011-05-20 12604.64 12630.11 12453.96 12512.04 4066020000 12512.04 5 2011-05-19 12561.46 12673.78 12506.67 12605.32 3626110000 12605.32 6 2011-05-18 12471.78 12595.60 12402.15 12560.18 3922030000 12560.18 # 日付と終値を抽出して、すべてのデータをデータフレームに統合 > dji <- with(dji.prices, rev(Close)) > dates <- with(dji.prices, rev(Date)) > comparison <- data.frame(Date = dates, MarketIndex = market.index, DJI = dji) > head(comparison) Date MarketIndex DJI 1 2002-01-02 30.11593 10073.40 2 2002-01-03 29.87794 10172.14 3 2002-01-04 29.68801 10259.74 4 2002-01-07 29.77801 10197.05 5 2002-01-08 28.97101 10150.55 6 2002-01-09 28.73909 10094.09
図にしてみます。
> ggplot(comparison, aes(x = MarketIndex, y = DJI)) + geom_point() + geom_smooth(method = 'lm', se = FALSE) > ggsave(filename="plot.png")
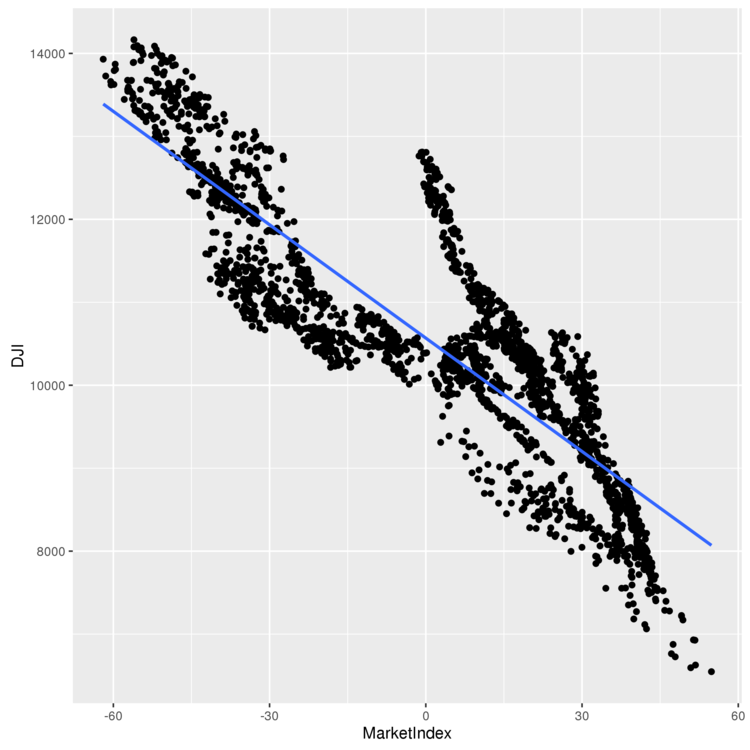
相関関係が見て取れるので、うまく要約できている感じです。
時間軸上で図にしてみてみる
最後に、作成した指標と、ダウ平均株価を時間軸上で並べて比較してみます。
# 指標の単位を合わせて比較しやすくする。また、正の相関になるように指標を調整 > comparison <- transform(comparison, MarketIndex = scale(MarketIndex)*-1) > comparison <- transform(comparison, DJI = scale(DJI)) > head(comparison) Date MarketIndex DJI 1 2002-01-02 -1.0346886 -0.3251888 2 2002-01-03 -1.0265119 -0.2602872 3 2002-01-04 -1.0199864 -0.2027079 4 2002-01-07 -1.0230787 -0.2439139 5 2002-01-08 -0.9953525 -0.2744783 6 2002-01-09 -0.9873846 -0.3115893 > alt.comparison <- melt(comparison, id.vars = 'Date') > names(alt.comparison) <- c('Date', 'Index', 'Price') > ggplot(alt.comparison, aes(x = Date, y = Price, group = Index, color = Index)) + geom_point() + geom_line() > ggsave(filename="plot2.png")
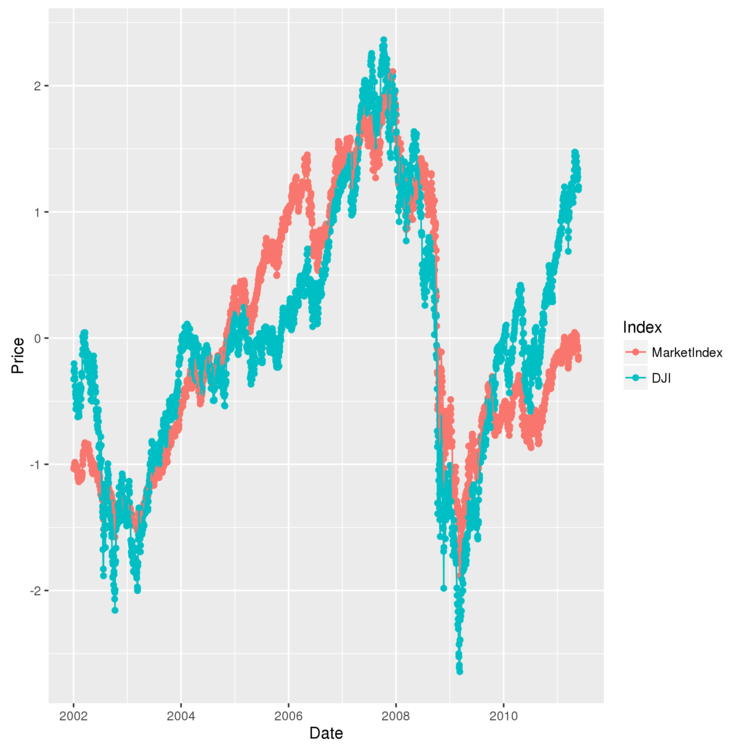
まぁ、こんなもんですかね。

