[Ruby]ダイクストラアルゴリズムでグラフデータ中の2点間の最短経路を算出する

ダイクストラアルゴリズムで、グラフデータ中の2点間の最短経路を算出してみます。

まずは、グラフのデータ構造を作成。とりあえずグラフの構築と探索に必要な最低限のAPIのみ用意しました。

Graph
- グラフです。
- verticesフィールドでグラフ中の頂点を配列で持ちます。
- Graph#add_vertexで頂点を追加できます。
  - 各頂点には、追加時にIDが割り振られます。
- Graph#connect,disconnectでグラフ中の頂点同士を接続できます。
  - 接続時には「重み」が指定でき、より軽い経路が最短とされます。
Vertex
- 頂点です。Graph#verticesで保持されるオブジェクトです。
- edgesフィールドで経路(接続されている頂点と経路の重みのペア)の配列を持ちます。

# グラフ
class Graph
  
  def initialize( directed=false )
    @serial = 0
    @directed = directed
    @vertices = []
  end

  def connect( from, to, weight=1 )
    assert_vertex_exist from
    assert_vertex_exist to
    @vertices[from].connect( to, weight )
    @vertices[to].connect( from, weight ) unless @directed
  end

  def disconnect( from, to )
    assert_vertex_exist from
    assert_vertex_exist to
    @vertices[from].disconnect( to )
    @vertices[to].disconnect( from, weight ) unless @directed
  end
  
  def add_vertex( data )
    id = @serial
    @serial += 1
    @vertices[id] = Vertex.new( id, data )
    return id
  end

  def inspect
    return "---\n" + vertices.collect {|v| v.inspect }.join("\n")
  end
  
  attr_reader :vertices
  
private
  def assert_vertex_exist( id )
    if ( id < 0 || id >= @vertices.length || !@vertices[id] )
      raise "vertex not exist. id=#{id}" 
    end
  end
  
end

# 頂点
class Vertex
  def initialize( id, data )
    @id = id
    @data = data
    @edges = []
  end
  def connect( to, weight )
    @edges.push({
      :to=> to,
      :weight=> weight
    })
  end
  def disconnect( to )
    @edges.reject! {|e| e.to === to }
  end
  def inspect
    return "#{@id}:#{@data.inspect}\n" + @edges.collect{|e|
        "  -> #{e[:to]} : #{e[:weight]}"
      }.join("\n")
  end
  attr_reader :id, :data, :edges
end

サンプルで使用するグラフは以下。

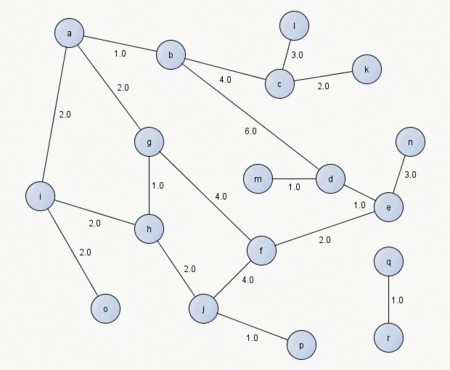
次のコードで生成できます。

graph = Graph.new

ids = []
('a'..'r').each{|i|
  ids << graph.add_vertex( i )
}
graph.connect(ids[0], ids[1], 1.0)
graph.connect(ids[0], ids[6], 2.0)
graph.connect(ids[0], ids[8], 2.0)
graph.connect(ids[1], ids[2], 4.0)
graph.connect(ids[1], ids[3], 6.0)
graph.connect(ids[2], ids[10], 2.0)
graph.connect(ids[2], ids[11], 3.0)
graph.connect(ids[3], ids[4], 1.0)
graph.connect(ids[3], ids[12], 1.0)
graph.connect(ids[4], ids[5], 2.0)
graph.connect(ids[4], ids[13], 3.0)  
graph.connect(ids[5], ids[6], 4.0)
graph.connect(ids[5], ids[9], 4.0)
graph.connect(ids[6], ids[7], 1.0)
graph.connect(ids[7], ids[8], 2.0)
graph.connect(ids[7], ids[9], 2.0)
graph.connect(ids[8], ids[14], 1.0)
graph.connect(ids[9], ids[15], 1.0)
graph.connect(ids[16], ids[17], 1.0)

ダイクストラアルゴリズムによる最短経路探索の流れは以下のとおり。

開始位置から隣接する頂点を、最も軽い経路を優先して順に探索していきます。
1. 例題の場合であれば、開始頂点である a の隣接頂点[b,g,i]をまず探索し、aからそれぞれの頂点までの重みを算出します。
  - 算出した重み、および、前の頂点のIDは、最短経路の算出時に使用するため、頂点ごとに記憶しておきます。
2. 次に、↑で探索された頂点のうち、最も短い=重みの合計値が低い経路である「b」の隣接頂点[c,d]を探索します。
  - 最も短い経路を順に処理するため、優先度つきキューを使用します。
3. bの探索が完了したら、次に軽い経路である「g or i」の隣接頂点を探索します。
4. 以上を順に繰り返し、常に最も短い経路を優先してすべての経路を探索していきます。
すでに探索済みの頂点に別のルートで再度到達した場合、より短い方の経路を採用し、記憶されている算出した重みと前の頂点のIDを更新します。
開始位置から到達可能なすべての頂点を探索すれば、処理はそこで終了。
- 目的の頂点に到達しても、他の経路のほうが短い可能性があるため、すべての経路の探索が完了するまで処理は継続されます。

実装は次のような感じになります。優先度つきキューの実装はpriority-queueを使用しました。

require 'graph'
require 'priority_queue'

# ダイクストラ アルゴリズムでノード間の最短経路を算出する
class ShortestPathFinder
  
  def initialize( graph )
    @graph = graph
  end
  
  # startからすべてのノードへの最短経路を探索する
  def traverse( start )
    initialize_state( start )
    @queue.push( start, 0 )
    while( vertex_id_and_distance = @queue.delete_min )
      visit_vertex(vertex_id_and_distance[0], vertex_id_and_distance[1])
    end
    return self
  end
  
  # 指定頂点までの最短パスを構築する。
  def shortest_path_to( vertex_id )
    raise "not traversed" unless @start
    path = []
    while( @previous.include?( vertex_id ) && vertex_id != @start )
      path.unshift(vertex_id)
      vertex_id = @previous[vertex_id]
    end
    return path
  end
  
private

  # 状態を初期化する
  def initialize_state(start)
    @queue = PriorityQueue.new
    @distances = {}
    @previous = {}
    @start = start
  end
  
  # 頂点を訪問する
  def visit_vertex( vertex_id, distance )
    @graph.vertices[vertex_id].edges.each {|e|
      to = e[:to]
      distance_of_next_node = distance + e[:weight]
      if ( not_visited_or_shorter_path?( to, distance_of_next_node ) )
        @previous[to] = vertex_id
        @distances[to] = distance_of_next_node
        @queue[to] = distance_of_next_node
      end
    }
  end
  
  # 訪問済みでない、またはより短いパスであるか評価する。
  def not_visited_or_shorter_path?( vertex_id, distance )
    return !@distances.include?(vertex_id) || @distances[vertex_id] > distance
  end

end

利用例。graph は↑で作成したものです。

finder = ShortestPathFinder.new( graph ).traverse(ids[0])
graph.vertices.each {|v|
  path = finder.shortest_path_to(v.id).collect{|id| 
    graph.vertices[id].data 
  }.join(' -> ')
  puts "#{v.data} : #{ path }"
}

実行結果です。到達不能なq,rのパスは空配列になります。

a : 
b : b
c : b -> c
d : b -> d
e : g -> f -> e
f : g -> f
g : g
h : g -> h
i : i
j : g -> h -> j
k : b -> c -> k
l : b -> c -> l
m : b -> d -> m
n : g -> f -> e -> n
o : i -> o
p : g -> h -> j -> p
q : 
r :